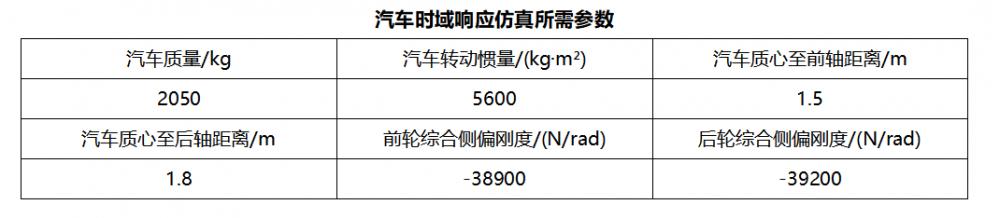
问题:利用汽车横摆角速度传递函数和质心侧偏角传递函数,对汽车时域响应进行仿真,绘制汽车横摆角速度和质心偏侧角的时域特性曲线。汽车时域响应仿真所需参数见下表。
取状态向量为X = [β ωr]’,输入向量U = [δ1],输出向量为Y = [β ωr]’,状态空间方程为:
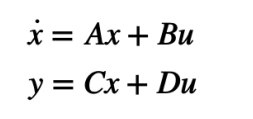
式中,A = [(K1+K2)/mu, (aK1 - BK2)/mu²-1; (aK1-bK2)/Iz, (a²K1+b²K2)/Iz*u] 称为系统矩阵;B = [-K1/mu; -aK1/Iz] 称为控制矩阵;C = [1 0; 0 1] 称为输出矩阵;D = [0; 0] 称为传递矩阵。
汽车速度分别选取20m/s、30m/s、40m/s;在仿真时间0s时给前轮一个阶跃信号,使前轮转角从0°转到10°,并保持不变。根据汽车状态空间模型,建立模型,绘制不同车速下的汽车横摆角速度和质心侧偏角的时域特性曲线。
首先:通过北太天元计算汽车状态空间方程的系统矩阵和控制矩阵,在北太天元依次输入下面语句;
>> m=2050;Iz=5600;a=1.5;b=1.8;L=3.3;
>> k1=-38900;k2=-39200;
>> u= [20 30 40];
>> a11 = (k1 + k2)/m./u;
>> a12 = (a*k1 - b*k2 -m.*u.^2)/m./u.^2;
>> a21 = (a*k1 - b*k2)/Iz;
>> a22=(a^2*k1 + b^2*k2)/Iz./u;
>> b11 = -k1/m./u;
>> b21 = -a*k1/Iz;
得到结果如下图1所示 ;
图1
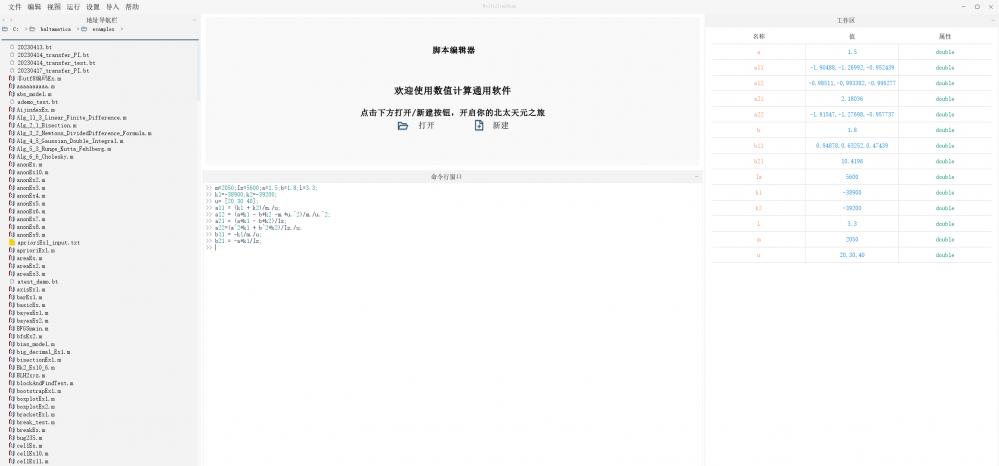
将命令行窗口,和工作区窗口放大后如图2、图3所示;

图2
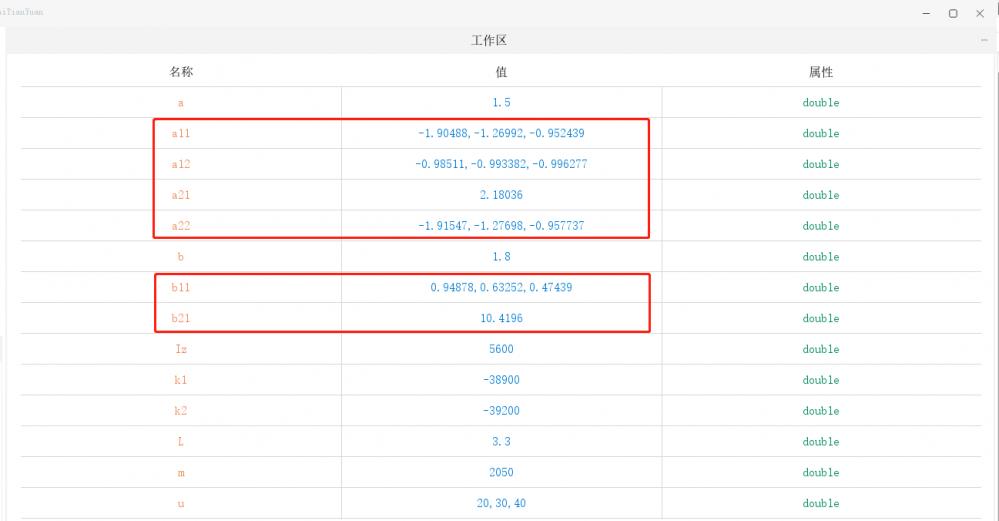
图3
因为,汽车状态空间方程的系统矩阵为:A = [a11, a12; a21, a22];控制矩阵为:B = [ b11; b21]; 所以,从图3红色框中可以得到各项系数如下:
当汽车速度 s = 20 m/s 时,系统矩阵:A = [-1.90488,-0.98511;2.18036,-1.91547]; 控制矩阵:B = [0.94878; 10.4196];
当汽车速度 s = 30 m/s 时,系统矩阵:A = [-1.26992,-0.993382;2.180436,-1.27698]; 控制矩阵:B = [0.63252; 10.4196];
当汽车速度 s = 40 m/s 时,系统矩阵:A = [-0.952439,-0.996277;2.180436,-0.957737]; 控制矩阵:B = [0.47439; 10.4196];
状态方程输出矩阵C = [1 0; 0 1];传递矩阵D = [0; 0]。
又因为,在仿真时间0s时给前轮一个阶跃信号,使前轮转角从0°转到10°;所以模型还需一个阶跃信号模块,阶跃时间=0;且,还需一个增益模块,增益= pi*10/180 = 0.1745。
通过北太真元建立汽车状态空间模型,如下图所示:
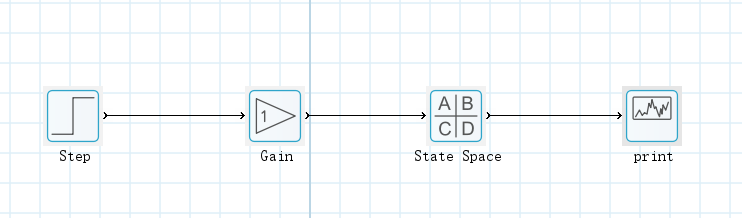
设置参数:仿真时长:10s;步长0.01s;求解器:ode4
得到的仿真结果,如下图所示:
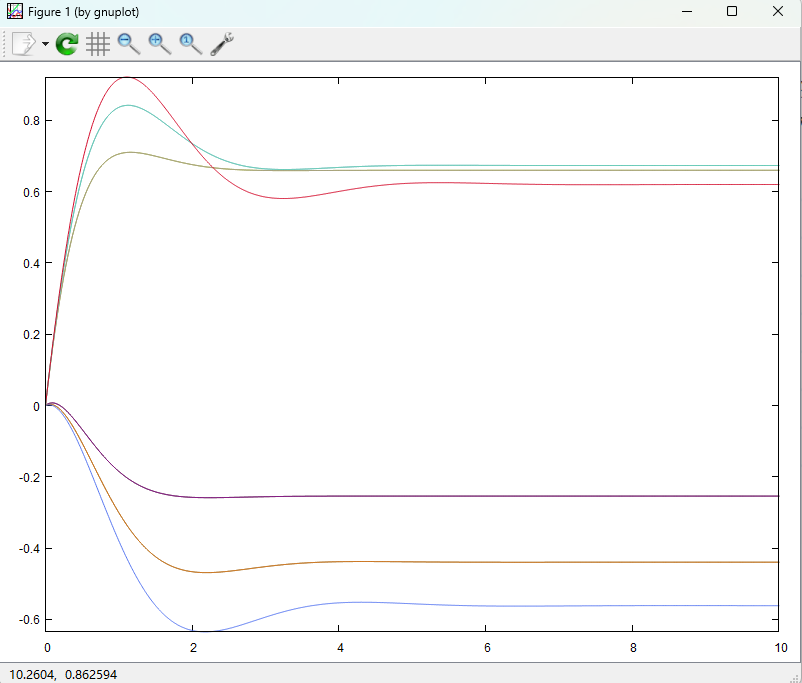
上半部分代表汽车横摆角速度时域特性曲线;即:
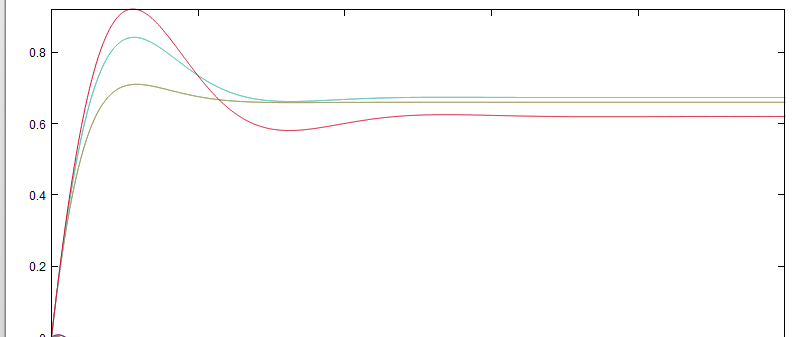
墨绿色代表速度20m/s时的特性曲线;
绿色代表速度30m/s时的特性曲线;
红色代表速度40m/s时的特性曲线。
下半部分代表汽车质心侧偏角时域特性曲线;即:
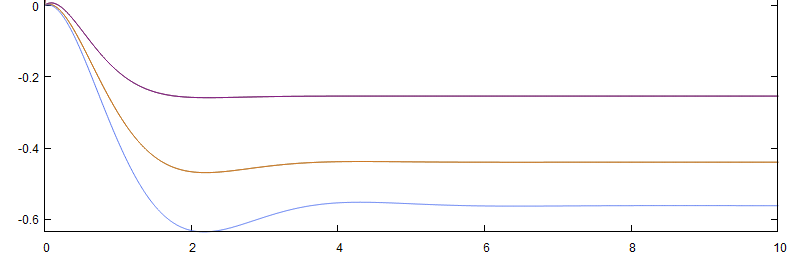
紫色代表速度20m/s时的特性曲线;
橙色代表速度30m/s时的特性曲线;
蓝色代表速度40m/s时的特性曲线。
