控制系统稳定与否是绝对稳定性的概念。而对一个稳定的系统而言,还有一个稳定的程度,即相对稳定性的概念。相对稳定性与系统的动态性能指标有着密切的关系。在设计一个控制系统时,不仅要求它必须是绝对稳定的,而且还应保证系统具有一定的稳定程度。只有这样,才能不致因系统参数变化而导致系统性能变差甚至不稳定。
对于一个最小相角系统而言,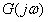 曲线越靠近
曲线越靠近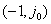 点,系统阶跃响应的振荡就越强烈,系统的相对稳定性就越差。因此,可用
点,系统阶跃响应的振荡就越强烈,系统的相对稳定性就越差。因此,可用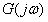 曲线对
曲线对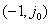 点的接近程度来表示系统的相对稳定性。通常,这种接近程度是以相角裕度和幅值裕度来表示的。
点的接近程度来表示系统的相对稳定性。通常,这种接近程度是以相角裕度和幅值裕度来表示的。
要计算相角裕度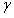 ,首先要知道截止频率
,首先要知道截止频率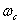 。求
。求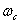 较方便的方法是先由
较方便的方法是先由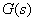 绘制
绘制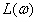 曲线,由
曲线,由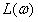 与
与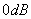 线的交点确定
线的交点确定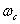 。而求幅值裕度
。而求幅值裕度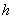 首先要知道相角交界频率
首先要知道相角交界频率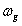 ,对于阶数不太高的系统,直接解三角方程
,对于阶数不太高的系统,直接解三角方程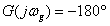 是求
是求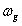 较方便的方法。通常是将
较方便的方法。通常是将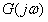 写成虚部和实部, 令虚部为零而解得
写成虚部和实部, 令虚部为零而解得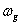 。
。
【例6-10】 某单位反馈系统的开环传递函数为:
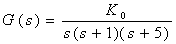
试求时系统的相角裕度和幅值裕度。将该开环传递函数变换为:
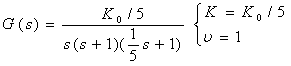
在实际工程设计中,只要绘出曲线即可。
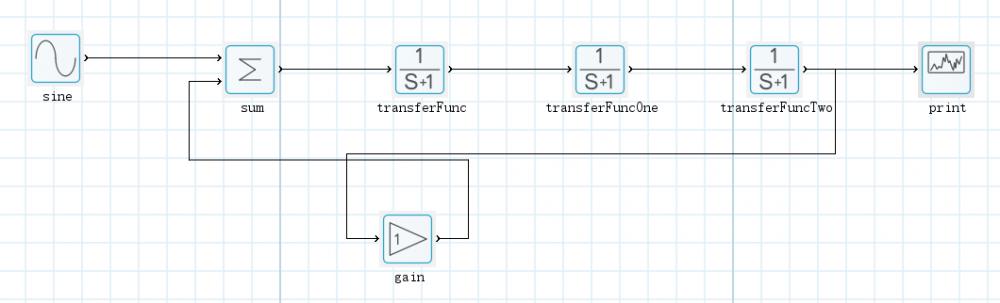
根据该传递函数模型,在北太真元搭建稳定裕度系统模型如下图所示:
设置仿真参数:
从上到下,传递函数参数依次为:
num = [52];den = [1 0];
num = [1];den = [1 1];
num = [1];den = [1 5];
仿真时长:10s;步长0.1s;求解器:ode4
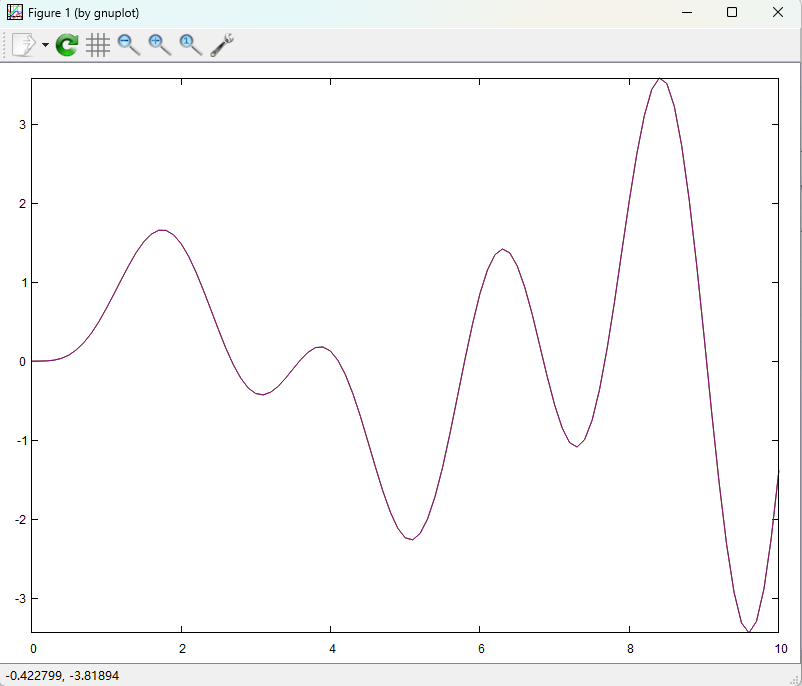
得到的仿真结果,如下图所示: