基于Baltamulink的衰减曲线法整定参数

基于Baltamulink的衰减曲线法整定参数

使用4:1衰减曲线法设计下列被控传递函数的PI控制器，分别计算P控制、PI控制的参数值，并绘制控制前后系统的单位阶跃响应曲线。4:1衰减法控制参数计算公式如下表所示：

4:1衰减法控制

被控传递函数方程如下：

Gp(s) =1 / 100^3 + 80^s + 17s + -1;

调节参数时，比例系数由小变大，并增加扰动观察响应过程，知道响应曲线峰值衰减比为4:1，记录此时的比例系数Kp为Ks，两个峰值之间的时间周期为周期Ts。

假设：响应曲线峰值衰减比为4:1时的比例系数 Ks= 4.74;

      两个峰值之间的时间周期 Ts = 21.9967；

则，按照上面4:1衰减法控制表中的计算公式可得：

P控制：比例系数 Kp = Ks = 4.74；

PI控制：比例系数 Kp = Ks/1.2 = 3.95；

            积分时间常数 Ti = 0.5 * Ts = 10.9984;

            积分系数 Ki = Kp / Ti = 3.95 / 10.9984 = 0.3591;

P（比例）控制

首先，把控制器设置成纯比例控制，即令积分系数Ki和微分系数Kd为零，在北太真元建立模型，形成比例控制系统，结构如下图所示；

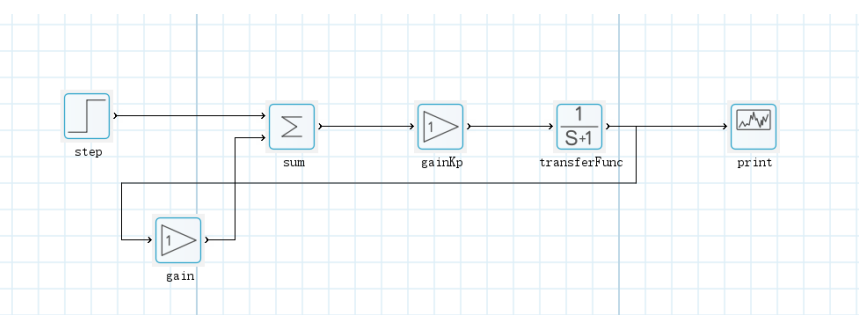
设置参数：

仿真时长：30s；步长0.01s；求解器：ode4

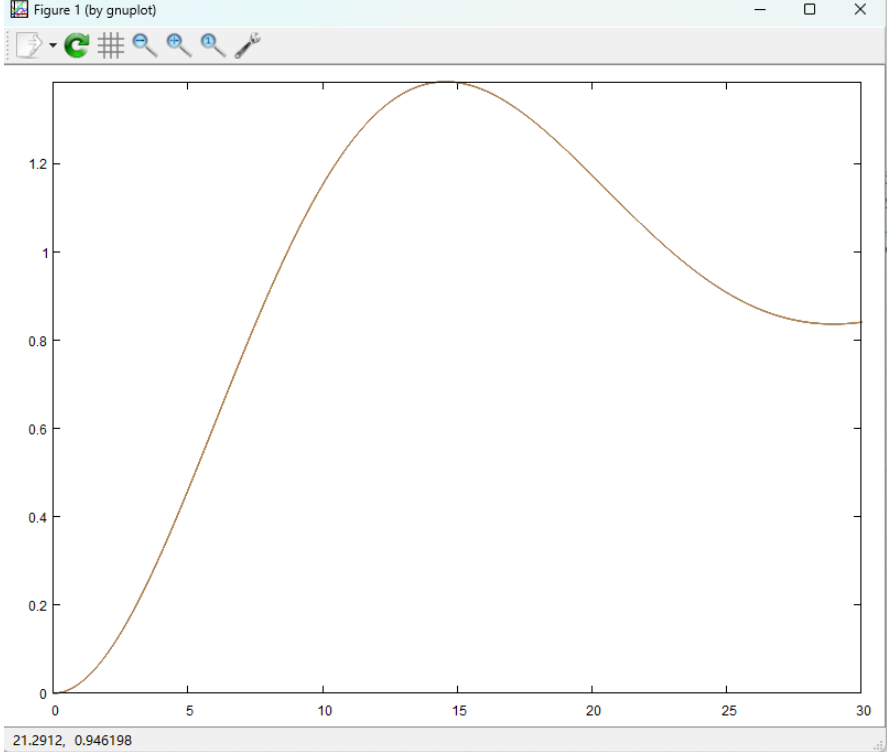
得到的仿真结果，如下图所示：

PI（比例积分）控制

首先，在纯比例控制系统的基础上增加积分系数Ki，令微分系数Kd为零，在北太真元建立模型，形成比例控制系统，结构如下图所示；

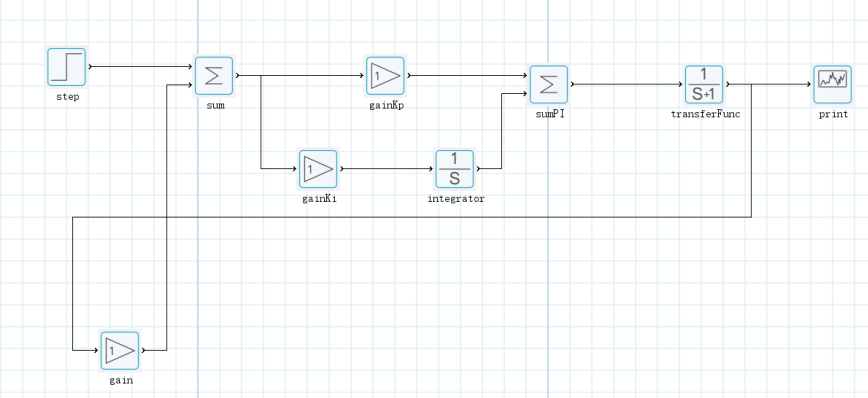
设置参数：

仿真时长：30s；步长0.01s；求解器：ode4

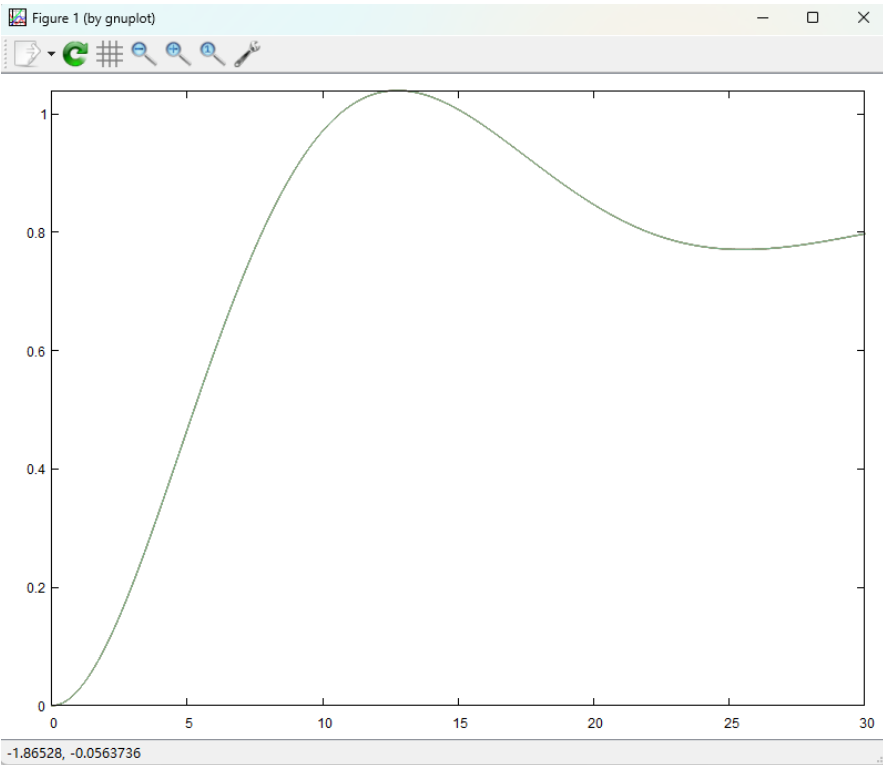
得到的仿真结果，如下图所示：