最小二乘法进行多项式拟合

一、 最小二乘原理介绍

最小二乘法是一种常见的数学方法，用于解决线性回归问题。它可以用来估计因变量（目标变量）与自变量之间的线性关系，即通过已知的一组数据来确定未知的回归方程。

具体来说，最小二乘法的目标是找到一条直线（或者更一般的曲线），使得这条直线与已知数据点的距离平方和最小。这条直线的方程称为回归方程，可以用来预测因变量的值。

最小二乘法的原理是通过最小化误差平方和来确定回归方程的系数。误差指的是已知数据点到回归直线的距离，也就是因变量的真实值与预测值之间的差异。通过最小化误差平方和，可以找到最优的回归系数，使得预测值与真实值之间的误差最小。

在实际应用中，最小二乘法常常用于数据拟合和预测。例如，在金融领域，最小二乘法可以用来预测股票价格和交易量；在工程领域，最小二乘法可以用来拟合实验数据和优化设计参数。

在计算中，最小二乘法可以通过矩阵运算来求解。具体来说，可以使用线性代数中的矩阵求解方法，例如求解矩阵的逆或者使用QR分解。在北太天元中，可以使用polyfit函数来实现最小二乘法求解线性回归问题。

二、 根据最小二乘原理进行多项式拟合

原始数据点为，根据最小二乘法进行多项式拟合：

(1) 设拟合多项式为

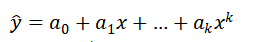
(2) 各点到这条曲线的距离之和，即误差平方和为：

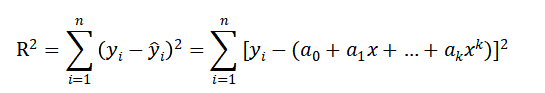
(3) 根据最小二乘原理，等式右边求ai偏导数：

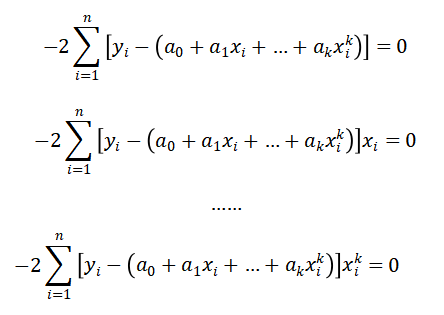
(4) 化简得：

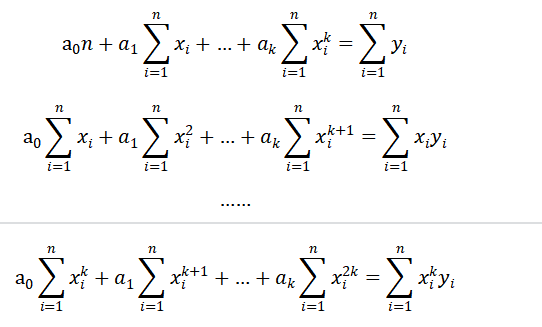
(5) 化成矩阵形式：

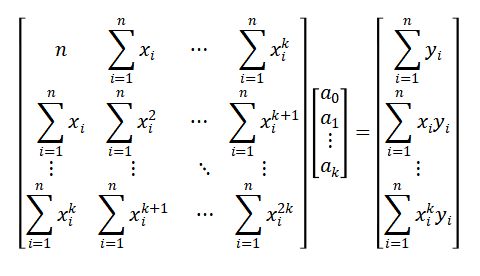
(6) 化简得

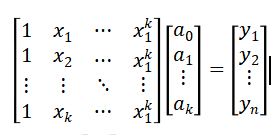
(7) 求解上述方程组，即可得到系数矩阵，从而得到拟合多项式。

三、 基于北太天元实现最小二乘法，并对比拟合结果与polyfit结果

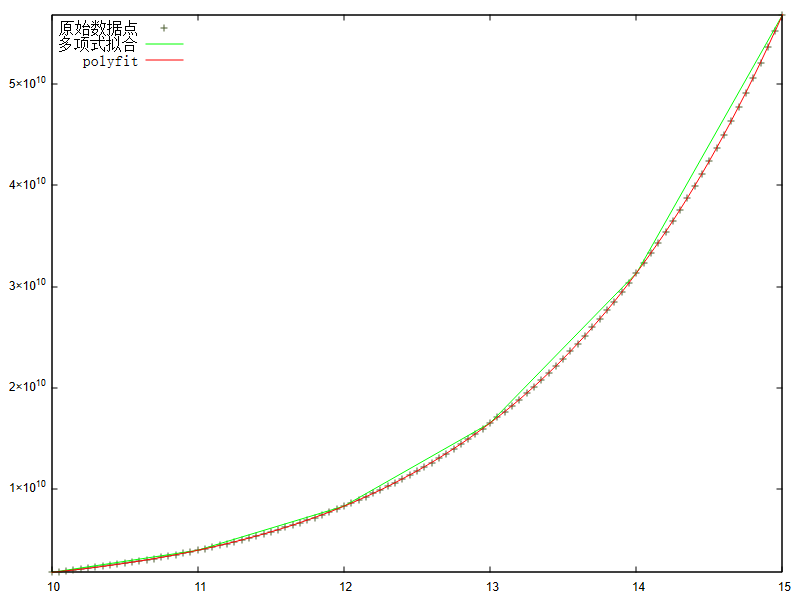
 附录代码：

clear all
close all
clc
N=10;%多项式阶数
%原始数据点
X=10:0.05:15;
M=length(X);
p=[5.6,2.5,3.3,0.18,0.29,2.4,4.8,1.2,7.1,1];
Y=zeros(1,M);
for i=1:10
    Y=Y+p(i)*X.^(i-1);
end
% Y=Y+unifrnd(-2e9,2e9,1,M);
%多项式拟合
X1=zeros(N+1,M);
for i=1:M
    X1(1,i)=1;
end
for i=2:N+1
    X1(i,:)=power(X,i-1);   %构造系数矩阵
end
XX=X1';
P_n=(XX'*XX)\XX'*Y';
X_n=min(X):max(X);
Y_n=zeros(1,length(X_n));
for i=1:N+1
    Y_n=Y_n+P_n(i)*X_n.^(i-1);
end
%polyfit
P=zeros(1,N);
P=polyfit(X,Y,N);
X_polyfit=zeros(1,M);
Y_polyfit=zeros(1,M);
X_polyfit=linspace(min(X),max(X),M);
Y_polyfit=polyval(P,X_polyfit);
figure(1);
plot(X,Y,'.');
hold on
plot(X_n,Y_n,'g');
hold on
plot(X_polyfit,Y_polyfit,'r');
legend('原始数据点','多项式拟合','polyfit','Location','northwest');