导语:
在教育不断改革与发展的当下,数学建模对于中学生的重要性日益凸显。教育部高度重视中学生数学建模能力的培养,相关政策不断出台,为数学建模教育的发展指明方向。同时,各类中学生数学建模赛事蓬勃开展,为学生提供了展示才能的广阔舞台。在这一浪潮中,北太天元科学计算软件(简称:北太天元)凭借其强大功能,成为助力中学生数学建模的得力助手。
政策引领
数学建模能力培养已成国家战略


教育部《2025年初中数学教学装备配置标准》及《2025年普通高中数学教学装备配置标准》明确指出,要推动科学计算、数学建模等核心素养的落地实施。文件中强调,数学实验与信息化工具的应用是 “教学装备现代化的重要方向”,需通过软硬件结合的方式,帮助学生 “直观理解抽象概念,提升解决实际问题的能力”。
以数学建模为例,政策要求中学阶段需引导学生 “从实际问题抽象数学模型,利用计算工具进行分析验证”,而这与北太天元的设计理念高度契合。北太天元支持从数据可视化、算法设计到模型验证的全流程操作,完全覆盖了初高中阶段数学建模教学的需求。
真实案例北太天元破解深圳中考 “排队论” 建模题
2025年深圳市初中学业水平考试以 “排队论” 为背景,要求建立数学模型分析最优配置方案。这一题目紧扣生活实际,旨在考查学生数据建模与算法实现能力。

北太天元迎战
北太天元团队运用软件的矩阵运算、离散事件仿真模块及可视化功能,成功实现了以下步骤:
01第1~2问
代码实现:
% 模型参数 channel = 3; % 通道数 per_channel_per_min = 6; % 每条通道每分钟通过人数 rate = channel * per_channel_per_min;
% 时间变量 x = 0:30;
% 现场总人数 y(x) y = -x.^2 + 60*x + 100;
% 已入场人数 entered = rate * x;
% 排队人数 queue = y - entered;
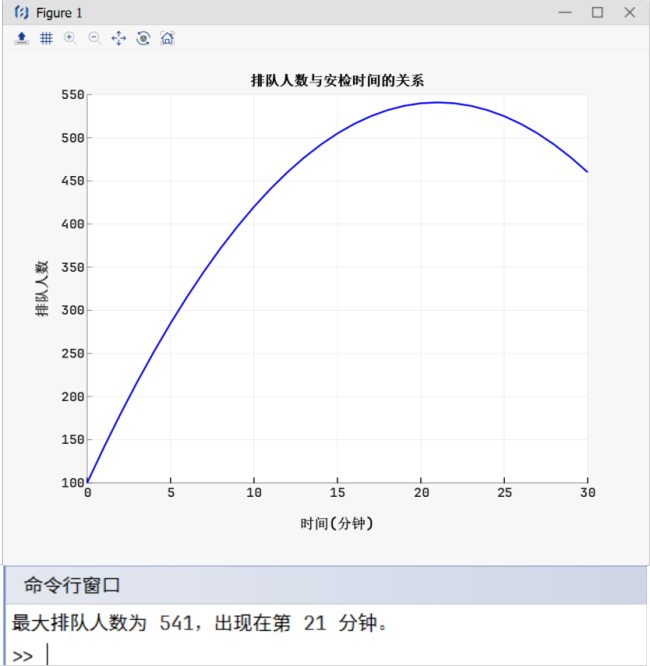
% 可视化 figure; plot(x, queue, 'b', 'LineWidth', 2); xlabel('时间(分钟)'); ylabel('排队人数'); title('排队人数与安检时间的关系'); grid on;
% 寻找最大值 [max_queue, max_index] = max(queue); max_time = x(max_index); fprintf('最大排队人数为 %d,出现在第 %d 分钟。\n', max_queue, max_time); |
运行结果:
02第3问(解法一遍历)
代码实现:
% 时间定义 x = 0:30;
% 初始化结果 min_valid_channels = -1;
% 初始化图像 figure; hold on;
% 用于绘图 colors = lines(9); plot_handles = gobjects(1,9); % 保存每条曲线的句柄 legend_labels = strings(1,9); % 图例文字
% 添加 10 分钟参考线 xline(10, '--k', '10分钟', ... 'LabelHorizontalAlignment', 'left', ... 'LabelVerticalAlignment', 'bottom', ... 'LineWidth', 1.5);
% 遍历 1~9 条通道 for n = 1:9 % 排队人数函数 q = -x.^2 + (60 - 6*n)*x + 100;
% 顶点位置 x_star = (60 - 6*n)/2;
% 判断是否满足条件 if min_valid_channels == -1 && 10 >= x_star min_valid_channels = n; end
% 是否为最小满足通道数 if n == min_valid_channels % 高亮显示 plot_handles(n) = plot(x, q, 'r-', 'LineWidth', 3); legend_labels(n) = sprintf('%d条通道(最小满足)', n); else plot_handles(n) = plot(x, q, 'Color', colors(n,:), 'LineWidth', 1.5); legend_labels(n) = sprintf('%d条通道', n); end end
% 图像格式 xlabel('时间(分钟)'); ylabel('排队人数'); title('不同通道数下的排队人数变化'); grid on;
% 正确设置 legend legend(plot_handles, legend_labels, 'Location', 'northwest');
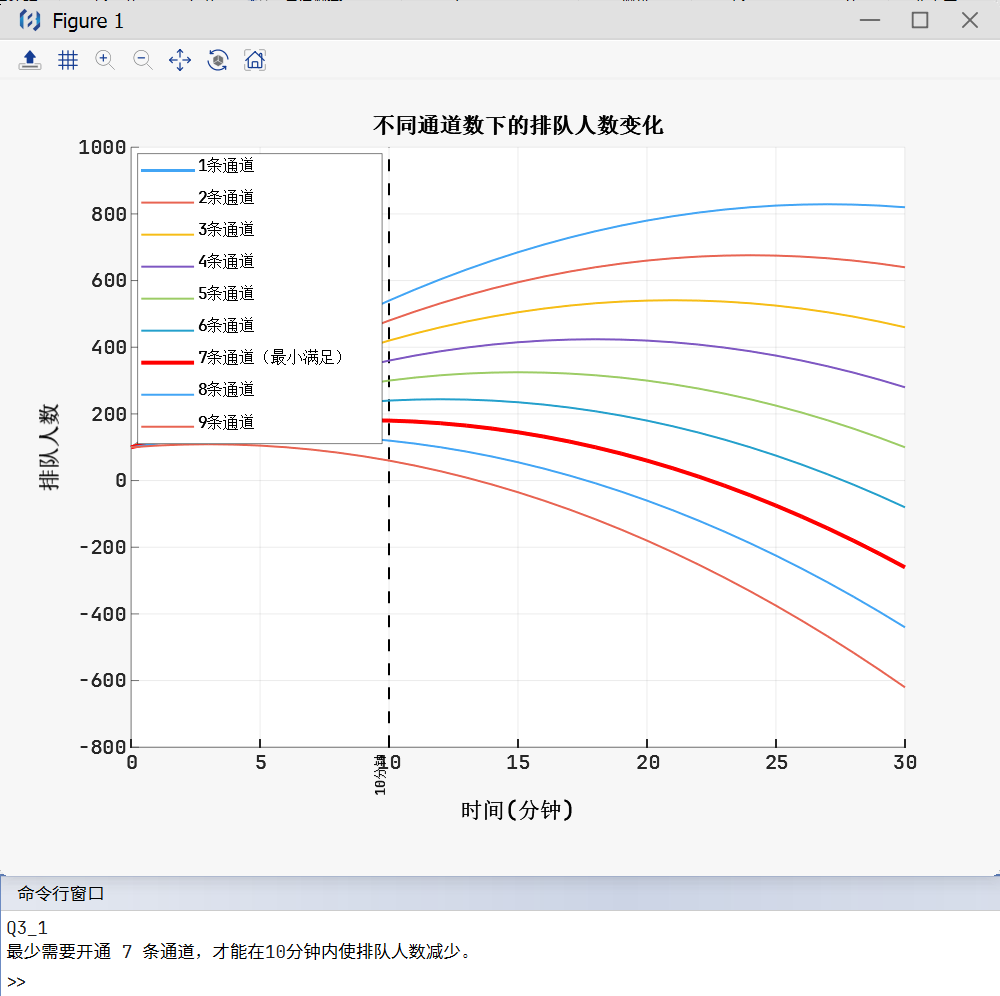
% 输出文字结果 if min_valid_channels == -1 fprintf('在最多开通 9 条通道的条件下,无法满足“10 分钟内排队人数减少”的要求。\n'); else fprintf('最少需要开通 %d 条通道,才能在10分钟内使排队人数减少。\n', min_valid_channels); end |
运行结果:
03第3问(解法二整数规划)
将问题整理成整数规划问题形式:
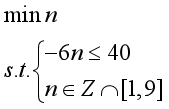
代码实现:
% 定义整数规划问题 f = 1; % 目标函数系数:最小化 n A = [-6]; % 不等式约束系数矩阵:-6n b = [-40]; % 不等式约束右侧:-40 lb = 1; % n 的下界 ub = 9; % n 的上界 intcon = 1; % 指定 n 为整数
% 求解整数规划 [x, fval] = intlinprog(f, intcon, A, b, [], [], lb, ub);
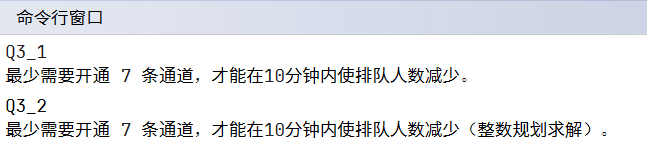
% 输出结果 fprintf('最少需要开通 %d 条通道,才能在10分钟内使排队人数减少(整数规划求解)。\n', x); |
运行结果:
04挑战升级:模型扩展
原始模型:
总观众人数随时间变化:
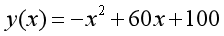
我们希望考虑以下现实因素:
· 观众到达过程为泊松分布(模拟不同时刻人流强度);
· 安检耗时为随机变量(服从正态分布);
· 队列容量有限,允许出现“溢出”;
· 演出开始时间固定(30分钟),需分析是否能及时入场;
· 动态控制通道数(如10分钟后增加通道);
1. 安检通道初始为 3 条,第 10 分钟后开放到 6 条;
2. 每条通道每分钟最多安检 6 人;
3. 每个观众的安检耗时服从 N(10s, 2s^2);
4. 模拟时间单位为秒,总时间为 1800 秒(30分钟);
5. 观众到达服从单位时间泊松过程,λ=1.5(平均每秒到达1.5人);
6. 队列最多容纳 500 人,超出视为“排队失败”;
代码实现:
% 模型参数 total_time = 1800; % 总时间:30分钟 = 1800秒 dt = 1; % 每秒更新 queue_limit = 500; % 队列容量限制
lambda = 1.5; % 泊松到达率(人/秒) mu = 1/10; % 平均安检服务率(每秒检1人/10秒)
% 初始化状态 queue = []; % 安检等待队列(存放等待时间) in_system = 0; % 当前队列人数 total_entered = 0; % 已入场观众数 overflow = 0; % 溢出人数
% 每条通道每秒最多服务1人,每人约用10秒 % 服务时间服从正态分布,记录每条通道的“忙碌时间” num_channels = 3; % 初始通道数 channels = zeros(1, 9); % 最多9条通道
% 数据记录 queue_record = zeros(1, total_time); entered_record = zeros(1, total_time);
for t = 1:total_time % 动态控制通道数:10分钟后增加到6条 if t == 600 num_channels = 6; end % 到达过程:泊松分布 arrivals = poissrnd(lambda); % 加入队列 for i = 1:arrivals if length(queue) < queue_limit queue(end+1) = normrnd(10, 2); % 每人需要的安检时间(秒) else overflow = overflow + 1; end end % 服务处理 for i = 1:num_channels if channels(i) <= 0 && ~isempty(queue) service_time = max(1, round(queue(1))); % 服务时长,不小于1 channels(i) = service_time; queue(1) = []; % 移除该观众 total_entered = total_entered + 1; end end % 更新各通道服务倒计时 channels = channels - 1; % 记录数据 queue_record(t) = length(queue); entered_record(t) = total_entered; end
% 可视化 time = (1:total_time)/60; % 转为分钟 figure; subplot(2,1,1); plot(time, queue_record, 'LineWidth', 1.5); xlabel('时间(分钟)'); ylabel('排队人数'); title('排队人数随时间变化');
subplot(2,1,2); plot(time, entered_record, 'LineWidth', 1.5); xlabel('时间(分钟)'); ylabel('累计入场人数'); title('入场人数随时间变化');
fprintf('30分钟内入场总人数:%d 人\n', total_entered); fprintf('排队溢出人数:%d 人\n', overflow); |
运行结果:
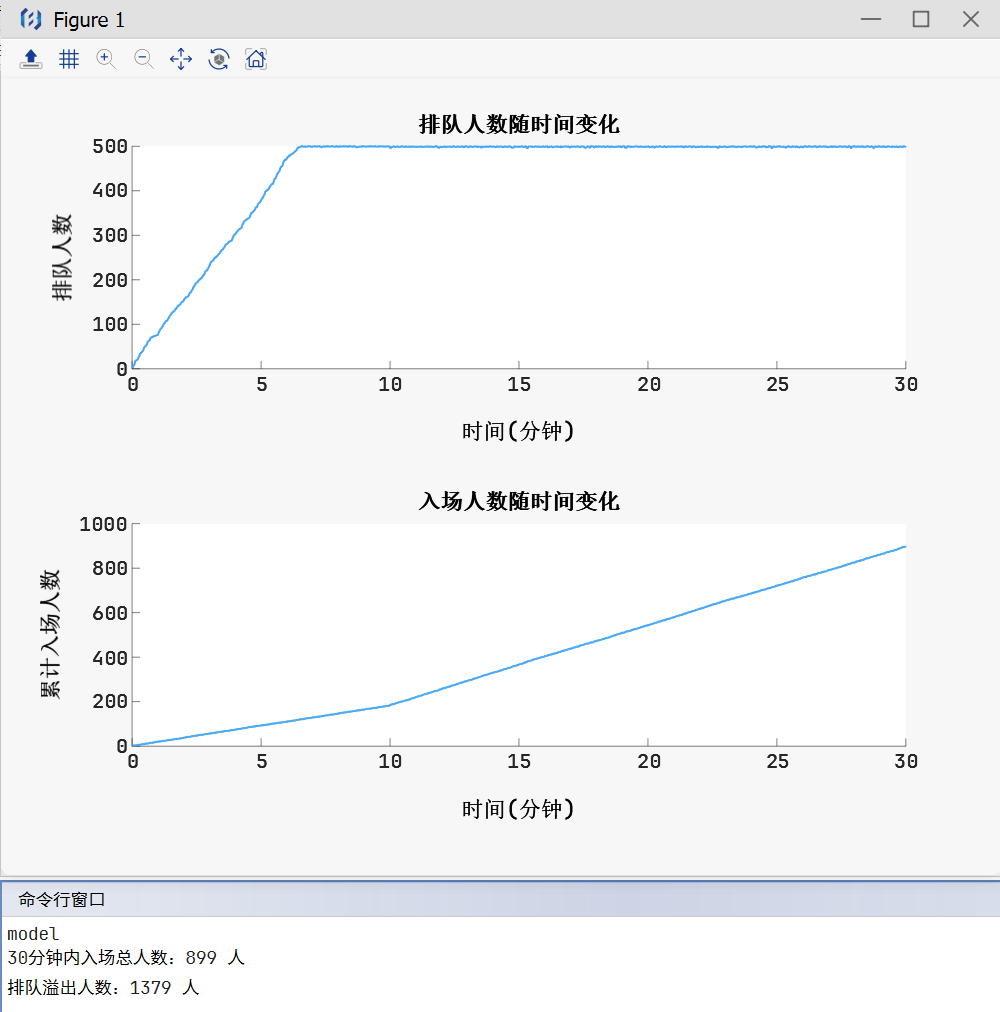
北太天元助力中学生数学建模的利器
近年来,数学建模能力培养已成为中学科创教育的重要组成部分。在教育部白名单赛事如全国青少年科技创新大赛中,建模与数据分析能力是学生解决实际问题(如环境治理、交通优化)的核心考察维度。同时,国内外学界广泛关注的数学建模实践活动(如美国高中生数学建模竞赛HiMCM等),也为中学生提供了跨学科实践平台。北太天元软件可无缝支持从算法设计到模型验证的全流程操作,助力学生在课堂学习与创新竞赛中高效达成目标,成为中学生的理想工具:
01强大的计算功能
强大的数值计算和符号计算能力,能够快速准确地处理复杂的数学运算。大大缩短计算时间,提高解题效率,让学生能够将更多的时间和精力投入到模型构建和问题分析中。
02丰富的函数库和工具箱
软件拥有丰富的函数库和工具箱,涵盖了数学、物理、工程等多个领域。这为学生解决不同类型的数学建模问题提供了便利。
03友好的交互界面和编程环境
具有友好的交互界面,操作简单易懂,即使是初次接触科学计算软件的中学生也能快速上手。
让工具赋能思维
用创新定义未来
北太天元软件凭借其强大的功能,可为中学生数学建模学习和实践提供有力支持。在教育部政策的引领下,结合丰富多样的数学建模赛事,北太天元将助力更多中学生提升数学建模能力,培养创新思维和实践能力,为未来的学习和发展奠定坚实的基础。无论是在课堂学习中,还是在参加各类数学建模赛事时,北太天元都将成为中学生不可或缺的得力工具,帮助他们在数学的海洋中探索前行,开启创新思维的大门。

点击直达:快来下载北太天元体验吧~https://www.baltamatica.com/download.html
-END-
如需合作,欢迎咨询

扫一扫添加企业微信
